Pass-Muraille
In modern day magic shows, passing through walls is very popular in which a magician performer passes through several walls in a predesigned stage show. The wall-passer (Pass-Muraille) has a limited wall-passing energy to pass through at most k walls in each wall-passing show. The walls are placed on a grid-like area. An example is shown in Figure 1, where the land is viewed from above. All the walls have unit widths, but different lengths. You may assume that no grid cell belongs to two or more walls. A spectator chooses a column of the grid. Our wall-passer starts from the upper side of the grid and walks along the entire column, passing through every wall in his way to get to the lower side of the grid. If he faces more than k walls when he tries to walk along a column, he would fail presenting a good show. For example, in the wall configuration shown in Figure 1, a wall-passer with k = 3 can pass from the upper side to the lower side choosing any column except column 6.
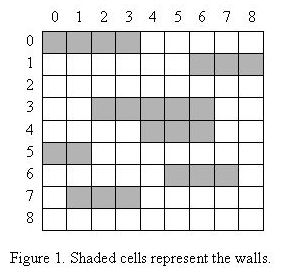
Given a wall-passer with a given energy and a show stage, we want to remove the minimum number of walls from the stage so that our performer can pass through all the walls at any column chosen by spectators.
The first line of the input file contains a single integer t (1 <= t <= 10), the number of test cases, followed by the input data for each test case. The first line of each test case contains two integers n (1 <= n <= 100), the number of walls, and k (0 <= k <= 100), the maximum number of walls that the wall-passer can pass through, respectively. After the first line, there are n lines each containing two (x, y) pairs representing coordinates of the two endpoints of a wall. Coordinates are non-negative integers less than or equal to 100. The upper-left of the grid is assumed to have coordinates (0, 0). The second sample test case below corresponds to the land given in Figure 1.
There should be one line per test case containing an integer number which is the minimum number of walls to be removed such that the wall-passer can pass through walls starting from any column on the upper side.
2 3 1 2 0 4 0 0 1 1 1 1 2 2 2 7 3 0 0 3 0 6 1 8 1 2 3 6 3 4 4 6 4 0 5 1 5 5 6 7 6 1 7 3 7
1 1
Walls are parallel to X.
Submit
